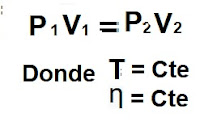https://www.youtube.com/watch?v=sOUQTUYCqH4
martes, 30 de junio de 2020
jueves, 25 de junio de 2020
miércoles, 24 de junio de 2020
martes, 23 de junio de 2020
viernes, 12 de junio de 2020
miércoles, 10 de junio de 2020
viernes, 5 de junio de 2020
TERCERA GUÍA GRADO ONCE 11°, FÍSICA, PROCESOS TERMODINÁMICOS.
INSTITUCION EDUCATIVA OCTAVIO
HARRY-JACQUELINE KENNEDY
|
||
Guía de aprendizaje por núcleos temáticos
|
---
Docente:
|
JORGE MARIO LÓPEZ GONZÁLEZ
|
Período:
|
2°
|
Año:
|
2020
|
---
Grado:
|
11°
|
Áreas por Núcleos Temáticos:
|
FÍSICA
|
---
Objetivos
de grado por núcleo temático:
|
1. Comprender la dinámica y adquirir conocimientos sobre la materia y
las propiedades de la misma, como parte del estudio de los objetos y las
sustancias y los cambios termodinámicos de ellos.
|
---
Competencias:
|
| 1.INTERPRETAR 2.ARGUMENTAR 3.PROPONER |
---
Indicadores
de desempeño:
|
|
1. Introducción:
TERMODINÁMICA
Rama de la
Física encargada del estudio de los cambios que sufren las sustancias cuando
cambian las variables termodinámicas, la presión, la temperatura, las moles y
el volumen. Aunque la termodinámica se encarga del estudio de cualquier clase
de sustancia, trabajaremos con gases que son las sustancias más fáciles de
tener cambios apreciables cuando cambian estas variables termodinámicas antes
nombradas.
Temperatura
Se designa
con la letra T mayúscula, es la medida de la energía cinética de las moléculas
o átomos de los que está hecha una sustancia o cuerpo. La temperatura se puede
medir en grados Celsius o Centígrados (°C) o en grados Fahrenheit (°F) o en
Kelvin (K).
Consulta 1: Averiguar las fórmulas para convertir
escalas de temperatura y aprender a usarlas.
Presión
Se designa
con la letra P mayúscula y es la fuerza ejercida sobre una sustancia o cuerpo
por unidad de área. La presión se mide en N/m2, que equivale a un
pascal (Pa), 1N/m2=1Pa. También son unidades de la presión, el
Torricelly (Torr), milímetros de mercurio (mm de Hg), Las atmósferas (atm), Los
PSI que es una medida inglesa que corresponde a libra sobre pulgada cuadrada,
esto es, “Pounds-force per square inch” (PSI). 1PSI = 1Lb/in2.
Consulta 2: Averiguar los factores de conversión de
presión, los que más pueda.
Volumen
El volumen
se designa con la letra V mayúscula, es el espacio que una sustancia ocupa en
el universo. Las unidades de volumen son, centímetro cúbico (cm3),
el metro cúbico (m3), el pie cúbico (ft3), la pulgada
cúbica (in3), el decímetro cúbico (dm3), el kilómetro
cúbico (Km3), el litro (L), el mililitro (mL), el centímetro cúbico
que también se puede llegar a encontrar así (cc), entre otras.
Consulta 3: Averiguar los factores de conversión de
medidas de volumen. Los que más pueda.
Moles
Se designa
con la letra griega eta minúscula (η), parecida a una
letra n nuestra. Representa la cantidad de materia que existe de una sustancia
en especial. Es una cantidad química, por tanto tiene que ver directamente con
la composición química de la sustancia tratada.
Ley general de gas ideal
Es una
correlación (fórmula) que relaciona todas las variables termodinámicas,
Presión, volumen, temperatura y moles.
Donde P es Presión
V
es Volumen
η es Moles
T es Temperatura
R Constante universal de los gases ideales
R Constante universal de los gases ideales
·
R = 0,0821 litros · atm / mol · K.
·
R = 8,3145 J / mol · K.
·
R = 8,2057 m 3 · atm / mol · K.
·
R = 62,3637 L · Torr / mol · K
· R = 62,3637 L · mmHg /
mol · K.
Procesos Termodinámicos
Son varios y
dependen de las variables termodinámicas relacionadas.
Proceso Isocórico
Proceso Isobárico
Proceso Isotérmico
Proceso Adiabático
Se presenta
cuando no hay pérdidas de calor al exterior del envase donde se realiza el
proceso. O sea, Q=0 J.
2. Comprensión
lectora:
1.
En un
procesos adiabático, entonces se supone que:
a. Las tres variables cambian.
b. Cambia solo la temperatura.
c. Cambia la temperatura y el volumen.
d. Cambian la presión y el volumen.
2.
En un proceso
isotérmico las variables P y V son:
a. Directamente proporcionales.
b. Constantes.
c. Cantidades decimales.
d. Inversamente proporcionales.
3.
La presión en
un procesos isobárico es:
a. Mayor que en un proceso isocórico.
b. Constante.
c. Inversamente proporcional a la temperatura.
d. Inversamente proporcional al volumen.
4.
La cantidad
de materia que se relaciona como moles en estos procesos, entonces, se puede
decir que:
a. Cambia pero no se sabe cómo.
b. Cambia poco.
c. No cambia durante el proceso.
d. No hay materia porque es un gas.
5.
Se llama
Isoterma a la línea que aparece en la gráfica de un proceso:
a. Isocórico.
b. Isobárico.
c. Adiabático.
d. Isotérmico.
3.
Actividades de profundización:
Ejercicios de profundización: En todos
los procesos se tomarán gases ideales para desarrollar el ejercicio.
- ¿En un
proceso adiabático cuál será el calor que pierde el sistema?
- En un
proceso isotérmico, cuyo volumen inicial es 20 L a una temperatura de 293
K y el volumen al que se lleva es 10 L, halle la nueva temperatura del
proceso.
- En un
proceso isocórico, la presión inicial es de 30 Pa y la final es de 20 Pa,
si la temperatura es de 300 K al terminar el proceso, ¿cuál seria la
temperatura al inicio del proceso?
- En un proceso isobárico, la presión es de 2 Atm, la temperatura inicial es de 293 K y la final es de 333 K, ¿Cuál sería entonces el volumen final si al principio estaba confinado en un envase de 2 L?
LA ACTIVIDAD CONSISTE EN TENER UN
RESUMEN DE ESTE DOCUMENTO EN EL CUADERNO, ADEMÁS, DE MANDAR FOTOS AL CORREO DE
LO QUE VA ADELANTANDO, EJERCICIOS Y CONSULTAS. SINO PUEDE ENVIAR AL CORREO,
DEBE DEJARLO EN EL CUADERNO HASTA QUE ÉSTE PUEDA SER REVISADO.
RECUERDEN QUE EL APRENDIZAJE DEPENDE
SOLAMENTE DE USTED Y QUE DEBE EVALUARSE USTED MISMO SOBRE LOS CONOCIMIENTOS QUE
ADQUIERE EN ESTE MOMENTO. LAS RESPONSABILIDAD ES SU PRINCIPAL HERRAMIENTA Y QUE
DE ACUERDO A ELLA USTED MEJORARÁ O NO SU CONOCIMIENTO EN TODAS LAS ÁREAS.
TERCERA GUÍA GRADO ONCE 11°, MATEMÁTICAS, ECUACIONES CUADRÁTICAS.
INSTITUCION EDUCATIVA OCTAVIO
HARRY-JACQUELINE KENNEDY
|
||
Guía de aprendizaje por núcleos temáticos
|
---
Docente:
|
JORGE MARIO LÓPEZ GONZÁLEZ
|
Período:
|
2°
|
Año:
|
2020
|
---
Grado:
|
11°
|
Áreas por Núcleos Temáticos:
|
MATEMÁTICAS
|
--
Objetivos
de grado por núcleo temático:
|
1. Conocer las inecuaciones, los conjuntos solución y las funciones
desde el punto de vista de las transformaciones por medio de operadores matemáticos
como la derivación y la integración, relacionándolas con las gráficas en el
plano cartesiano.
|
---
Competencias:
|
| 1.INTERPRETAR 2.ARGUMENTAR 3.PROPONER |
--
Indicadores
de desempeño:
|
|
1- Resuelve inecuaciones cuadráticas. 2- Entiende y aplica dominio y rango de funciones. 3- Comprende y grafica funciones polinómicas. 4- Comprende y grafica funciones cuadráticas. 5- Comprende y grafica funciones racionales. |
1. Introducción:
ECUACIÓN CUADRÁTICA
Una ecuación
cuadrática es aquella igualdad en la que se tiene una variable, llamada
incógnita a la que debemos averiguar, esa variable normalmente se representa
con una letra x, aunque podría ser cualquier letra. Una ecuación cuadrática
tiene que ver directamente con una función cuadrática y la gráfica de una
función cuadrática se llama parábola. La ecuación cuadrática es de la forma: ax2 + bx +
c = 0,
donde a, b y c son
números reales (Cualquier clase de número) y a debe ser diferente de cero (0).
Una ecuación
cuadrática tiene como solución los valores que puede tomar la x para que esa
igualdad a cero se respete.
Número de soluciones de la ecuación cuadrática
- Dos soluciones
- Una única solución.
- Ninguna solución.
- Factorizando. Usar la factorización
para hallar las soluciones posibles a la ecuación.
FACTORIZAR TRINOMIOS
·
Trinomio
cuadrado perfecto:
·
De los números d y e es
necesario que: (±d)(±e)=c y ±d ± e = ±b
·
Trinomio de la forma ax2+bx+c:
En este caso
no que tenemos que hacer es convertir este caso en el anterior
Aquí se debe tener en cuenta que d y e, resultan de la
factorización del trinomio de la forma x2+bx+c, como se muestra aquí,
y que se obtiene al multiplicar por a y dividir por a. Al final obtenemos dos paréntesis después de simplificar
y quitar la a del denominador.
- Despejando en caso de que se pueda.
Los casos en
los que se puede simplificar son aquellos en los que encontramos la ecuación
cuadrática así:
·
ax2=0
·
ax2+c=0
DESIGUALDADES CUADRÁTICAS
Se presentan cuando
una desigualdad tiene una letra elevada al cuadrado, a la 2, como mayor
exponente, esto es parecido a una ecuación cuadrática, pero con los símbolos de, “mayor que” ＞, o “menor que” ＜, o "Mayor o igual que" ≥, o "menor o igual que" ≤. La solución de una desigualdad de
esta clase es muy parecida a la solución de una ecuación cuadrática, usando los
métodos mostrado anteriormente para ecuaciones cuadráticas. De igual manera el
objetivo es encontrar el conjunto de números que satisfacen la inecuación.
Se recomienda para
estos casos de desigualdades utilizar la factorización o el despeje para efectuar
los ejercicios.
Ejemplo de
desigualdad:
Resolver: 3x2-14 ≤ -2 solución:
Ejemplo de
desigualdad:
Resolver: x2-2x-3 > 0 solución: x2-2x-3 > 0
Factorizamos trinomio
de la forma ax2+bx+c, así: (x-3)(x+1)>0 Aquí tenemos dos opciones
Para que sea mayor
que cero deben ser o, primero, los dos signos positivos o, segundo, los dos signos
negativos, así:
2. Comprensión
lectora:
1.
Las
soluciones de una ecuación cuadrática pueden ser:
a. Dos soluciones.
b. Una única solución.
c. No tener solución.
d. Todas las anteriores.
2.
Se llama
ecuación cuadrática a la que tiene la variable:
a. Elevada a la 2 como máximo exponente.
b. Elevada a la 2 o a la 1 como exponentes.
c. Elevada a la 2 y a la 1 como exponentes.
d. Elevada a cualquier valor, pero que tenga
factorización.
3.
La fórmula
general sirve para:
a. Resolver una ecuación cualquiera.
b. Resolver una inecuación cualquiera.
c. Resolver una ecuación cuadrática.
d. Resolver problemas de matemáticas.
4.
La
factorización de trinomios es muy útil para resolver:
a. Ecuaciones.
b. Ecuaciones e inecuaciones.
c. Inecuaciones.
d. Ecuaciones e inecuaciones cuadráticas.
5.
En las
inecuaciones aparecen los siguientes signos, EXCEPTO:
a. Igual (=).
b. Mayor que (>).
c. Menor que (<).
d. Menor o igual que (≤).
3.
Actividades de profundización:
Realiza los
ejercicios siguientes en el cuaderno mostrando los procedimientos para obtener
tu respuesta.
a.
x2 – 9 ＞ 0
b.
x2 + 3x ≥10
c.
x2 −
8x ＞ – 8 – 2x
d.
x2 – 4x
+ 3 ≥ – 6x + 2
e.
– x2 +
3x – 7 ≥ 0
f.
4x2 – 16
≤ 0
LA ACTIVIDAD CONSISTE EN TENER UN
RESUMEN DE ESTE DOCUMENTO EN EL CUADERNO, ADEMÁS, DE MANDAR FOTOS AL CORREO DE
LO QUE VA ADELANTANDO, EJERCICIOS Y CONSULTAS. SINO PUEDE ENVIAR AL CORREO,
DEBE DEJARLO EN EL CUADERNO HASTA QUE ÉSTE PUEDA SER REVISADO.
RECUERDEN QUE EL APRENDIZAJE DEPENDE
SOLAMENTE DE USTED Y QUE DEBE EVALUARSE USTED MISMO SOBRE LOS CONOCIMIENTOS QUE
ADQUIERE EN ESTE MOMENTO. LAS RESPONSABILIDAD ES SU PRINCIPAL HERRAMIENTA Y QUE
DE ACUERDO A ELLA USTED MEJORARÁ O NO SU CONOCIMIENTO EN TODAS LAS ÁREAS.
Suscribirse a:
Entradas (Atom)