|
|
INSTITUCION EDUCATIVA OCTAVIO
HARRY-JACQUELINE KENNEDY
|
|
|
Guía de aprendizaje por núcleos temáticos |
---
|
Docente: |
JORGE MARIO LÓPEZ GONZÁLEZ |
Período: |
3° |
Año: |
2020 |
---
|
Grado: |
11° |
Áreas por Núcleos
Temáticos: |
MATEMÁTICAS |
---
|
Objetivos de grado por núcleo
temático: |
|
1. Conocer las inecuaciones, los conjuntos solución y
las funciones desde el punto de vista de las transformaciones por medio de
operadores matemáticos como la derivación y la integración, relacionándolas
con las gráficas en el plano cartesiano. |
---
|
Competencias: |
|
1. CONCEPTUAL 2. PROCEDIMENTAL 3 ACTITUDINAL |
---
|
Indicadores de desempeño: |
|
1- (CONCEPTUAL) Comprende el concepto de derivada. 2- (PROCEDIMENTAL) Evalúa derivadas de diferentes funciones. 3- (ACTITUDINAL) Entiende la importancia de conocernos con nuestras fortalezas y nuestras debilidades. |
FECHAS: Octubre 1 al 22.
1. Introducción:
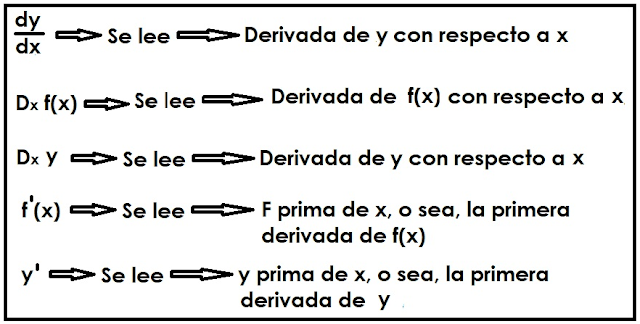
OPERADOR DERIVADA
La derivada es un operador matemático, un
operador es un símbolo o serie de símbolos que implican una alteración de
alguna manera a una cantidad o a una expresión matemática. El operador derivada
se simboliza de varias formas, así:
La derivada se aplica siempre, a una función,
las funciones pueden ser de cualquier clase. Derivar implica un cambio en la
función completamente.
La primera función que veremos es la función constante y la derivada cambia la función como se muestra en la figura de derivada de una función constante.
En esta derivada podemos observar cuando aparece una variable con o sin exponente, lo que debemos hacer para derivar.
En esta forma observamos cómo derivar una función logarítmica simple.
Si x no es sólo la variable, sino que es una
función debo derivar esa función y multiplicarla por la derivada.
En esta forma observamos cómo podemos derivar una función exponencial simple.
Si x no es sólo la variable, sino que es una función debo derivar esa función y multiplicarla por la derivada.
Aquí tenemos la función exponencial cuando la base es diferente del número Euler y la manera como se debe derivar.
Si x no es sólo la variable, sino que es una
función debo derivar esa función y multiplicarla por la derivada.
Una de las propiedades de las derivadas está esta, derivada de una suma.
Otra propiedad importante de las derivadas.
Una propiedad muy importante es ésta que damos en este numeral.
2. Comprensión lectora:
1. La derivada es:
a.
Una propiedad
de las funciones.
b.
Una función.
c.
Un proceso
para cambiar las funciones.
d.
Un operador
matemático.
2. La derivada
de una función exponencial se puede decir que:
a.
No altera la
función.
b.
Altera la función
y ésta cambia.
c.
La función se
altera elevándola al cuadrado.
d.
A la x se le
resta 1 y se divide por el exponente restándole 1.
3. Para aplicar
el operador derivada se utiliza:
a.
Límites para
obtenerla.
b.
Propiedades.
c.
Otro operador
cualquiera.
d.
El operador
multiplicación o suma.
4. La derivada
de una función constante es, siempre:
a.
0
b.
La misma
función.
c.
Elevar la constante
al cuadrado y restarle 1.
d.
1
5. Para hallar
la derivada usando límites se escribe Δx tendiendo a:
a.
0
b.
1
c.
La derivada.
d.
Al límite por
la izquierda y por la derecha.
3. Actividades de profundización:
Halle las derivadas de las siguientes funciones,
muestre los procedimientos para hallar su respuesta..
LA ACTIVIDAD CONSISTE EN TENER UN RESUMEN DE ESTE DOCUMENTO EN EL CUADERNO O COPIA DEL MISMO PEGADA EN ÉL, ADEMÁS, DEBE MANDAR FOTOS AL CORREO, jomalogo2@gmail.com, DE LOS EJERCICIOS Y CONSULTAS. SI NO PUEDE REALIZAR LAS CONSULTAS, POR FALTA DE INTERNET, AL MANDAR EL TRABAJO DEBE ESPECIFICAR QUE NO TIENEN ACCESO A MEDIOS DE CONSULTA.
“Definir tu propósito
es el punto de partida de todo logro.”
W. Clement Stone